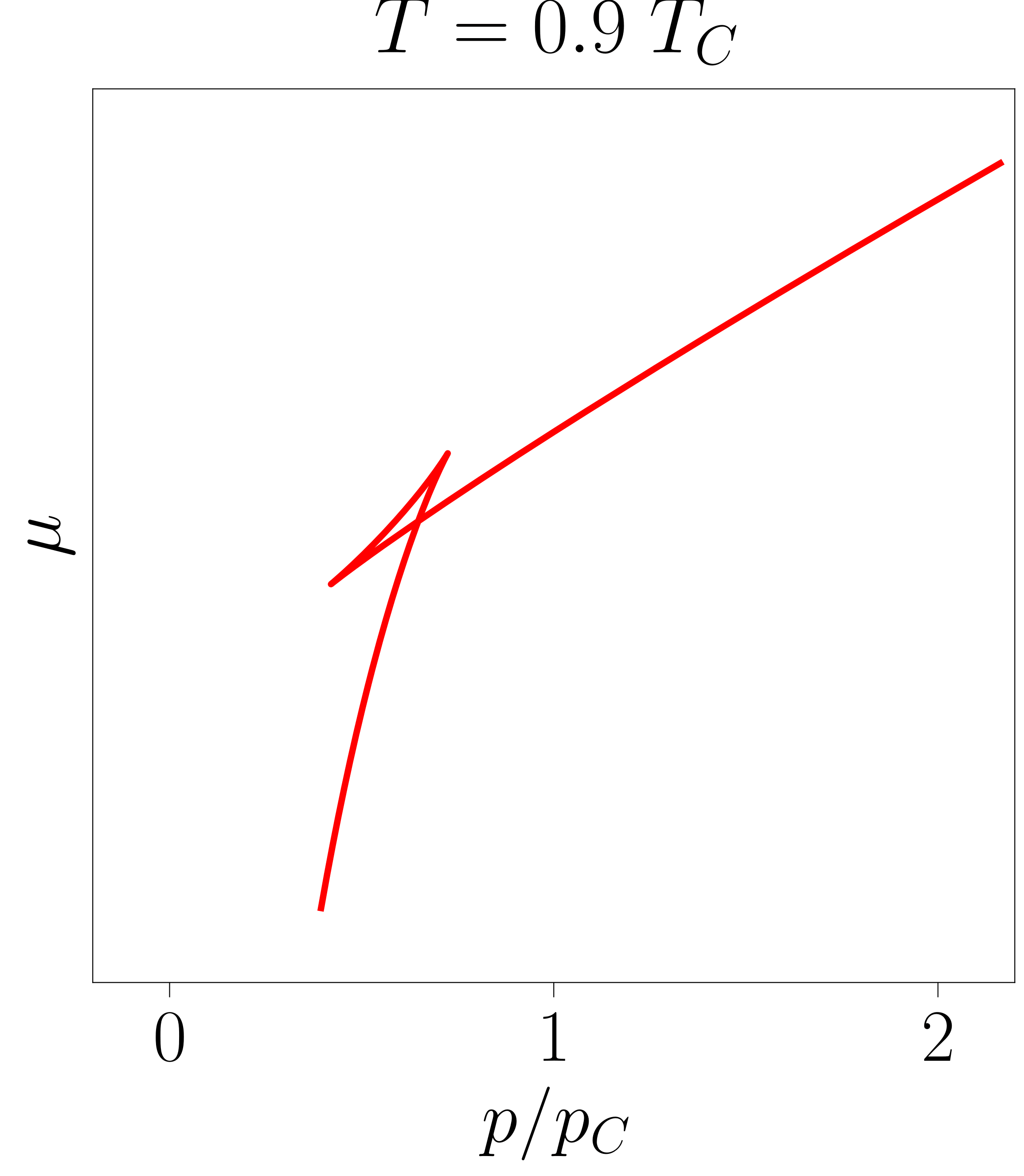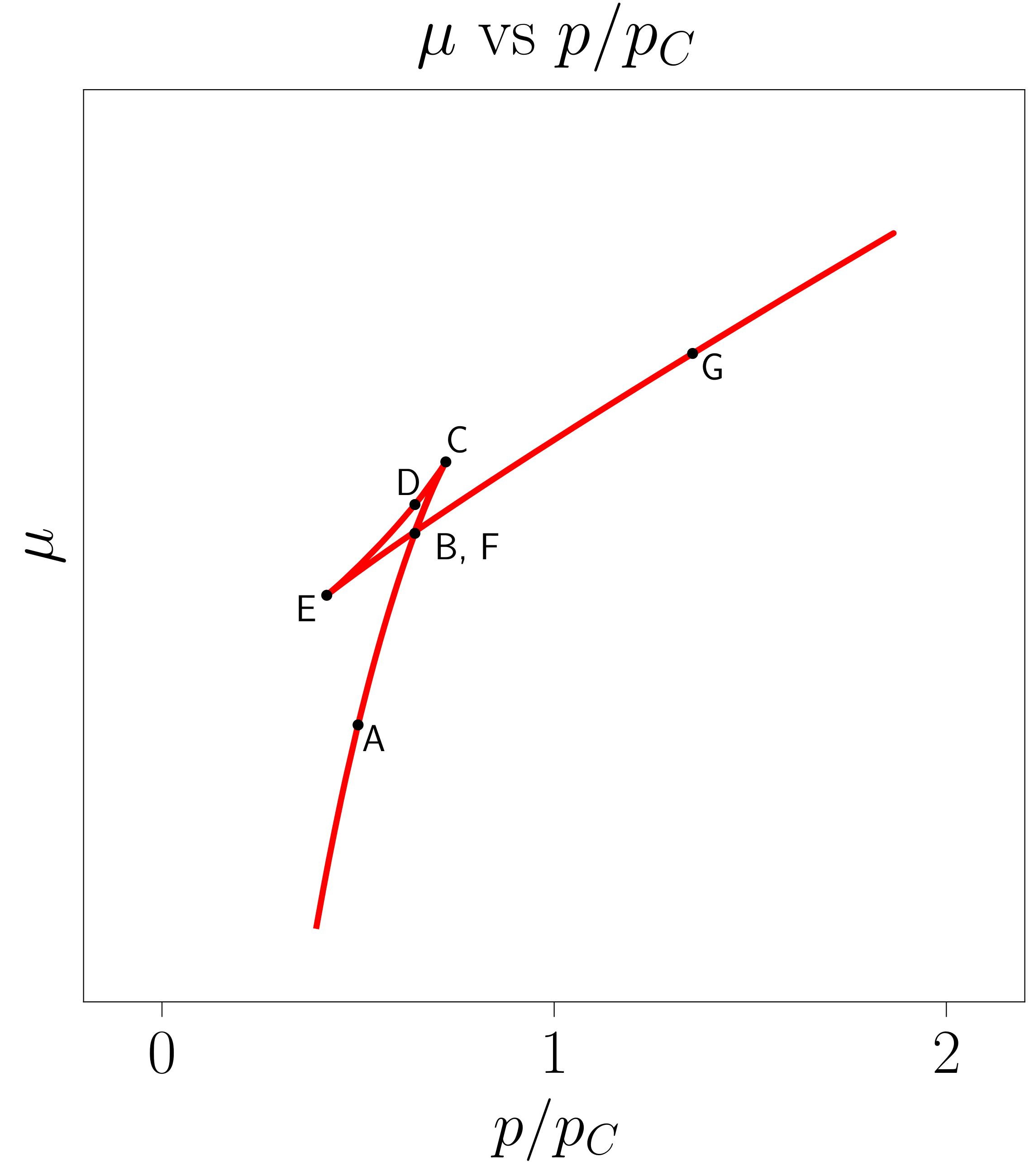van der Waals-en egoera-ekuazioa¶

Azalpen guztiak Josu M. Igartua irakasleak gainbegiratu ditu.

Nahiz eta fase-trantsizioen atzean dagoen oinarri fisikoa potentzial kimikoaren topologia izan, sarritan sistema termodinakoen azterketa lerro isotermoen forman oinarritzen da. Jariakin baten kasuan, oso interesgarria da van der Waals-en egoera-ekuazio mekanikoa (ikus \ref{vdw-eq-1}. ekuazioa) betetzen duen jariakin errealaren kasua aztergaitzat hartzea.

\begin{equation}\label{vdw-eq-1} \left( p + \frac{a}{v^2} \right)\left(v - b \right) = R T \end{equation}

non \(a\) eta \(b\) van der Waals-en parametroak, \(v\) jariakinaren bolumen molarra, \(p\) presioa, \(T\) tenperatura eta \(R\) gas idealen konstantea diren.

Gas idealen egoera-ekuazio mekanikoaren moldaketa bat bezala uler daiteke J.D. van der Waals herbeheretar fisikariak bere tesian proposatutako ekuazioa [1].

\begin{equation}\label{vdw-eq-2} pv = RT \end{equation}

Gas idealen egoera-ekuazioa (ikus \ref{vdw-eq-2}. ekuazioa) gas partikulak puntualak eta elkarren artean elkarrekintzarik gabekoak izatetik ondorioztatzen da. Van der Waals-en egoera ekuazioak, aldiz, bi faktore horiek kontuan hartzen ditu gas idealaren ekuazioari bi atal gehituz: \(a\) parametroarekiko proportzionala denak partikulen arteko elkarrekintza integratzen du eta \(b\) parametroak, aldiz, partikulek espazioan betetzen duten bolumena adierazten du [3]. Konposatu bakoitzerako bi parametro horien balioa esperimentalki lor daiteke.

Van der Waals-en arabera, jariakina osatzen duten partikulen bolumena zein haien arteko elkarrekintza berdina da sistemaren likido eta gas faseetan eta bi faseetako portaera bere egoera-ekuazioaren bidez deskriba daiteke, ondorioz. Are gehiago, ekuazioa bi faseetan baliagarria denez, bien arteko trantsizioak deskribatzeko ere baliagarria izango da.

Aipatu beharra dago egoera-ekuazio horrek ez duela jariakin errealen portaera modu kuantitatibo batean azaltzen, baina bai erabilgarria dela azalpen kualitatibo edota erdi-kuantitatiboak emateko.

Funtzioaren analisi-matematikoa lerro isotermoetan oinarritutako azterketaren abiapuntua izan daiteke, proposatutako funtzioak ez baitauka esangura fisikorik bere izate-eremu guztian. Lerro isotermoen adierazpena \ref{vdw-eq-1}. ekuaziotik ondoriozta daiteke.

\begin{equation}\label{vdw-eq-3} p(v ; T) = \frac{RT}{v - b} - \frac{a}{v^2} \end{equation}

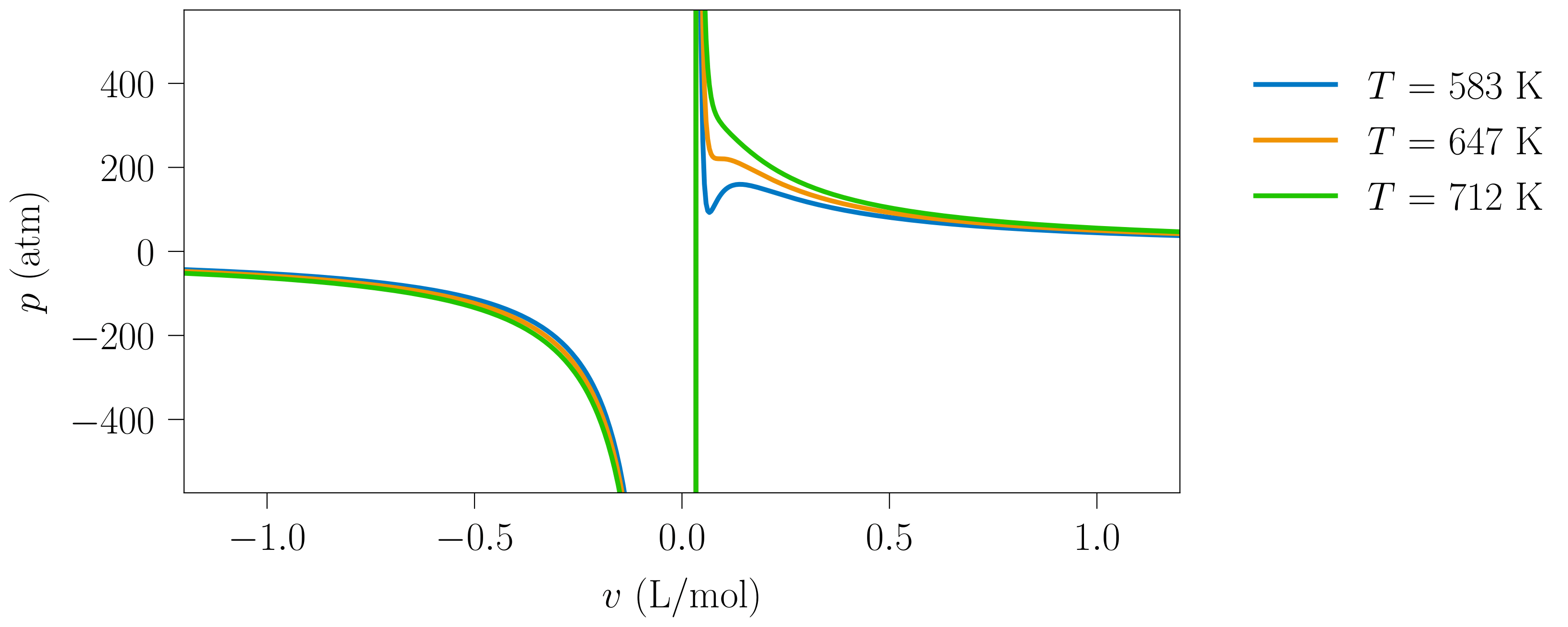
Begi-bistakoa denez, lerro isotermoen funtzioak polo bana du \(v=0\) eta \(v=b\) puntuetan, \ref{vdw-eq-3}. adierazpenak erakusten duen moduan. Edozein elementurentzat \(T\) tenperaturako lerro isotermoa \(v > 0\) eremuan irudikatuz (ikus 1. irudia) aipagarria da \(v \in (0, b)\) tartean \(\left(\partial p / \partial v \right)_{T} > 0\) dela. Sistema ezengonkorra da tarte horretan, egonkortasun-baldintzen arabera. Zonalde ezegonkor hori bi poloen artean mugatuta dagoenez, ez da posible sistema fisikoa eremu horretan egotea. Ondorioz, van der Waals-en egoera ekuazioak esangura fisikoa duen eremua \(v \in (b, \infty)\) da eta hori izango da hemendik aurrera aztertuko dena.

irudia: van der Waals-en egoera-ekuaziotik lortutako lerro isotermoen itxura. Irudia 118-000 programarekin sortu da.

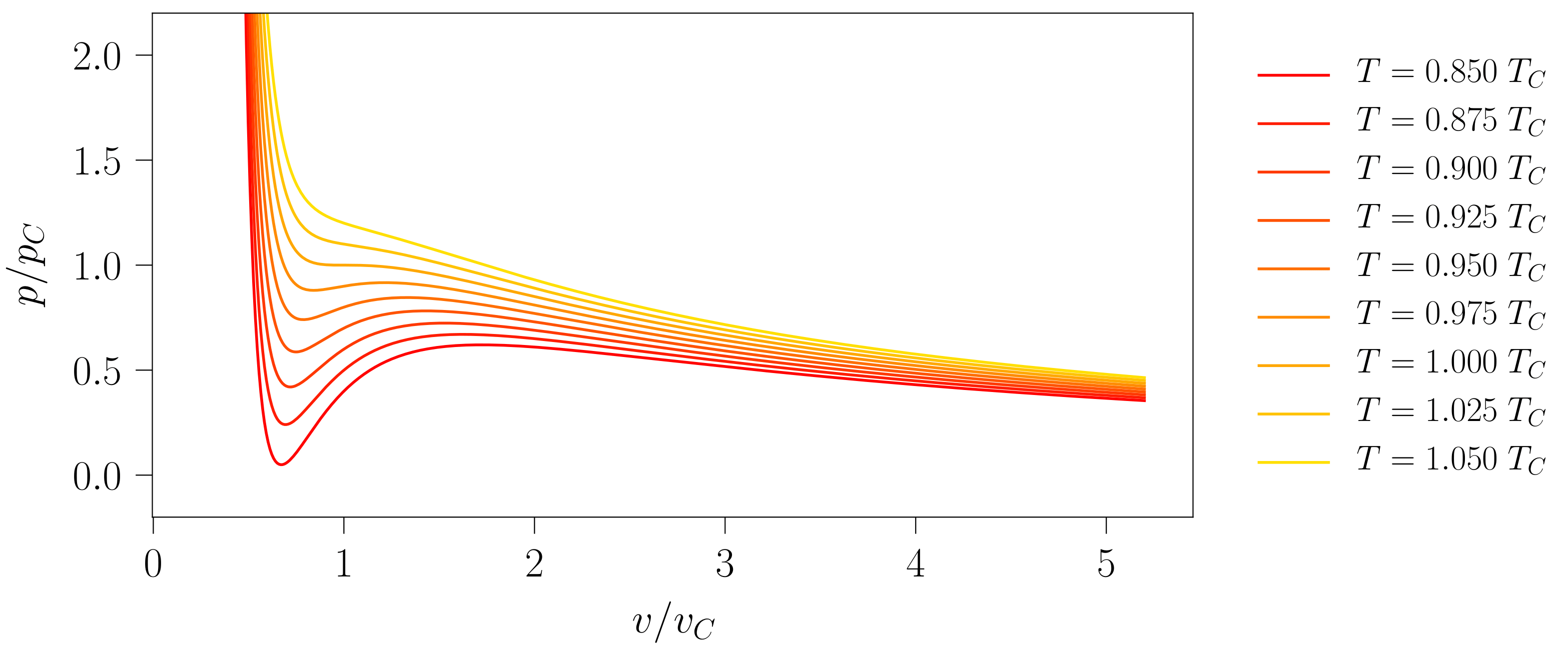
Eremu horren barruan lerro isotermo ezberdinak irudikatzean, nabarmena da bi zonalde ezberdintzen direla (ikus 2. irudia). Tenperatuta baxuetan agertzen den zonaldean lehen aipatutako egonkortasun-baldintzak huts egiten duen eremuak identifika daitezke eta, beraz, tenperatura horietan sistemak lehen ordenako fase-trantsizio bat jasaten duela ondoriozta daiteke. Tenperatura altuetan aldiz, sistema egonkorra da eremu guztian.

irudia: van der Waals-en egoera-ekuaziotik lortutako lerro isotermoen itxura. Irudia 111-000 programarekin sortu da.

Puntu kritikoa¶

Van der Waals-en egoera-ekuazioak lehen ordenako fase-trantsizioak aurreikusten dituenez, onargarria da puntu kritikoaren existentzia ere aurreikusi dezakeela pentsatzea. Kasu honetan, nahikoa da hurrengo baldintzak aplikatzea puntu kritikoa kalkulatzeko (baldintza orokorra potentzial kimikoaren ordena guztietako deribatuak nuluak izatea da):

\begin{equation}\label{vdw-eq-4} \left( \frac{\partial^2 \mu}{\partial p^2}\right)_{T} = 0 \quad \text{eta} \quad v \equiv \left( \frac{\partial \mu}{\partial p}\right)_{T} \; \rightarrow \quad \left( \frac{\partial^2 \mu}{\partial p^2}\right)_{T} \equiv \left( \frac{\partial v}{\partial p}\right)_{T} = 0 \end{equation}

\begin{equation}\label{vdw-eq-45} \left( \frac{\partial^3 \mu}{\partial p^3}\right)_{T} = 0 \quad \rightarrow \quad \left( \frac{\partial^3 \mu}{\partial p^3}\right)_{T} \equiv \left( \frac{\partial^2 v}{\partial p^2}\right)_{T} = 0 \end{equation}

Puntu kritikoaren adierazpena \ref{vdw-eq-4} eta \ref{vdw-eq-45} adierazpenetako baldintzak \ref{vdw-eq-3}. ekuazioko lerro isotermoari aplikatzean lortzen da:

\begin{equation}\label{vdw-5} p_C = \frac{a}{27 b^2} \qquad v_C = 3b \qquad T_C = \frac{8 a}{27 b} \end{equation}

Tenperatura kritikoko lerro isotermoa lerro isotermo kritikoa izango da eta horrek bananduko ditu 2. irudian ageri diren bi zonaldeak [3].

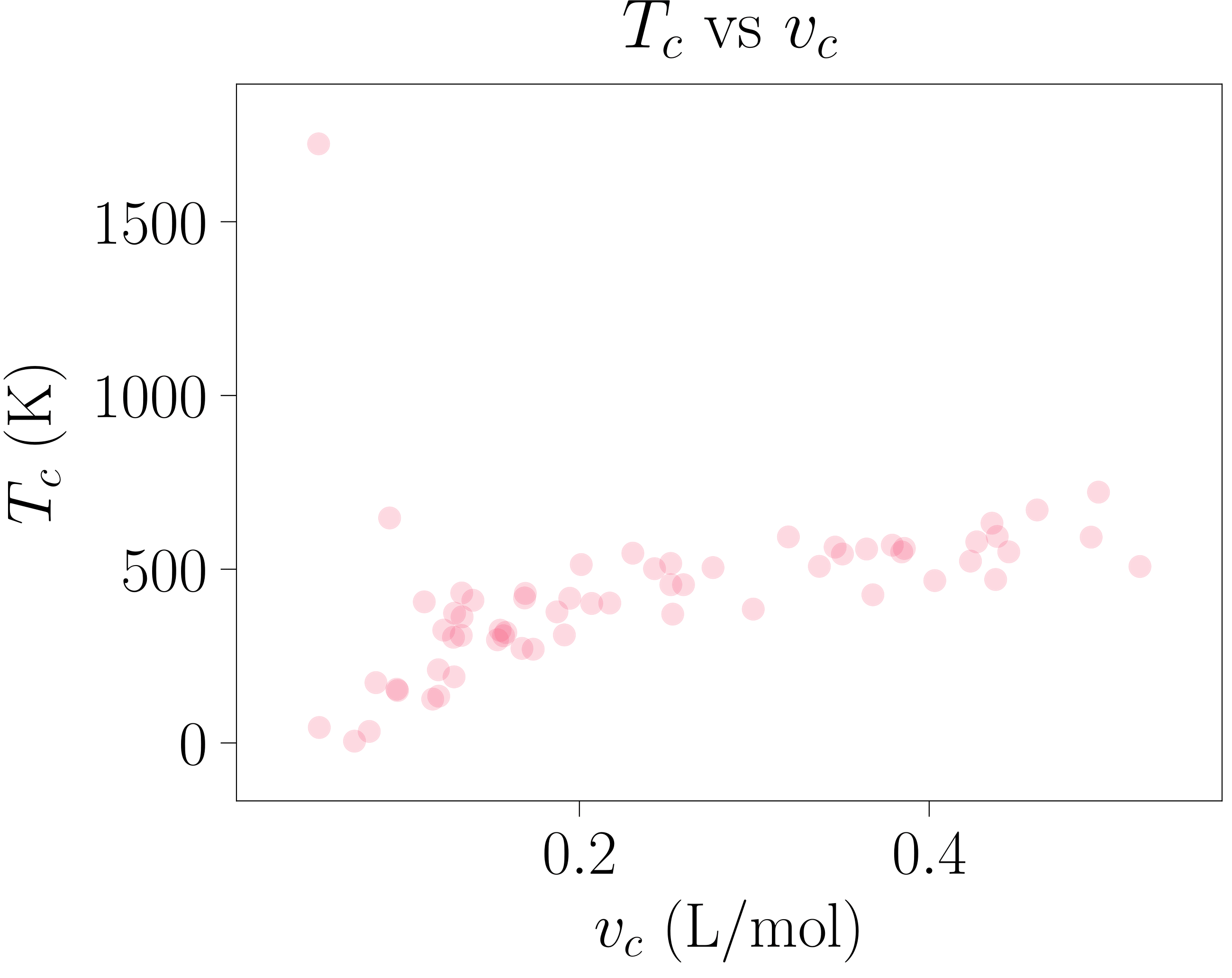
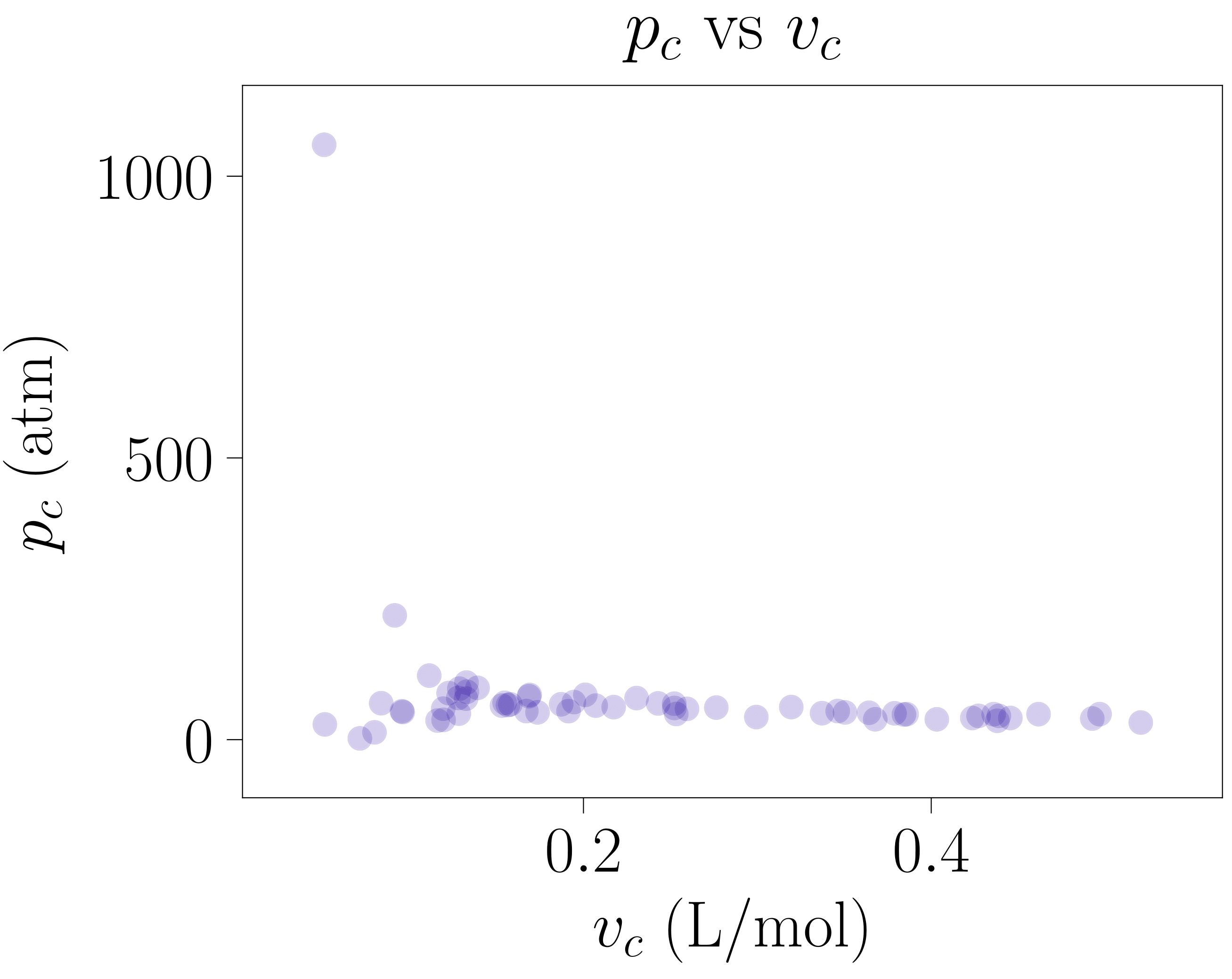
Van der Waals-en egoera-ekuazioko \(a\) eta \(b\) parametroak deskribatutako jariakinaren partikulen bolumenarekin eta haien arteko elkarrekintzarekin erlazionatuta daudenez, jariakin bakoitzarentzat bakarrak eta bereizgarriak dira. Puntu kritikoaren kokapena bi parametro horien menpekoa baino ez denez, jariakin bakoitzaren puntu kritikoa konfigurazio-espazioko puntu ezberdin batean egongo da kokatuta. Hori bistaratzeko 113-000 programa garatu da: ohiko elementu eta konposatuen parametroen balioak jasotzeaz gain haien puntu kritikoak grafika ezberdinetan erakusten ditu (ikus 3. irudiko grafikak).

irudia: Elementu eta konposatu batzuen puntu kritikoak. Parametroen balioak “CRC Handbook of Chemistry and Physics” liburutik atera dira [4]. Irudia 113-000 programarekin sortu da.

Puntu kritikoaren kokapena aztertutako jariakinaren menpekoa izateak, tenperatura berdinerako elementu bakoitzaren lerro isotermoek forma ezberdina azaltzea eragiten du (hori 113-000 programan ere behatu daiteke). Hala ere, behin puntu kritikoaren adierazpena ezagututa, posible da egoera-ekuazioa puntu kritikoaren menpe adieraztea:

\begin{equation} \left(p_R + \frac{3}{v_R^2}\right)\left(3 v_R - 1 \right) = 8 T_R \qquad \text{non} \qquad p_R = \frac{p}{p_C} \quad v_R = \frac{v}{v_C} \quad T_R = \frac{T}{T_C} \end{equation}

Ekuazio horri egoera-ekuazio laburtua deritzo eta jariakin guztietarako komuna da, ez baitu \(a\) eta \(b\) parametroekiko menpekotasun espliziturik [2]. Forma laburtua oso erabilgarria da adierazpen-grafikoak eta garapenak egiterako orduan, orokortasunik galdu gabe manipulatu beharreko parametroen kopurua murrizten baita eta, gainera, sistema guztiak aldi berean azaltzen baitira. Horregatik, hemendik aurrera adierazpen horretatik lortutako lerro isotermoak aztertuko dira (ikus \ref{vdw-8}. ekuazioa).

\begin{equation}\label{vdw-8} p_R \left(v_R, T_R \right) = \frac{8 T_R}{\left(3 v_R - 1 \right)} - \frac{3}{v_R^2} \end{equation}

Potentzial kimikoaren azterketa¶

Fase-trantsizioen inguruko teoria orokorrak van der Waals-en egoera-ekuazioan duen eragina aztertzeko, \(\mu\) potentzial kimikoaren adierazpena lortu behar da. Horretarako, \ref{vdw-6}. adierazpeneko Gibbs-Duhem-en erlaziotik abiatuz lerro isotermoan zehar tenperatura konstantea dela aplika daiteke integrala ebazteko:

\begin{equation}\label{vdw-6} d \mu = -s \; dT + v \; dp \; \xrightarrow{T = \text{kte}} \; \left( d \mu \right)_T = v \; \left( dp \right)_T \end{equation}

\begin{equation}\label{vdw-7} \mu = \int v \; dp + \phi (T) \end{equation}

non \ref{vdw-7}. adierazpeneko \(\phi (T)\) gaia integrazio-konstantea den, tenperaturaren menpekoa. Gai horren ondorioz, metodo horren bidez lortutako \(\mu = \mu(p, T)\) planoa ez da kuantitatiboki baliagarria izango, beti faltako baitu konstante horren ekarpena [2].

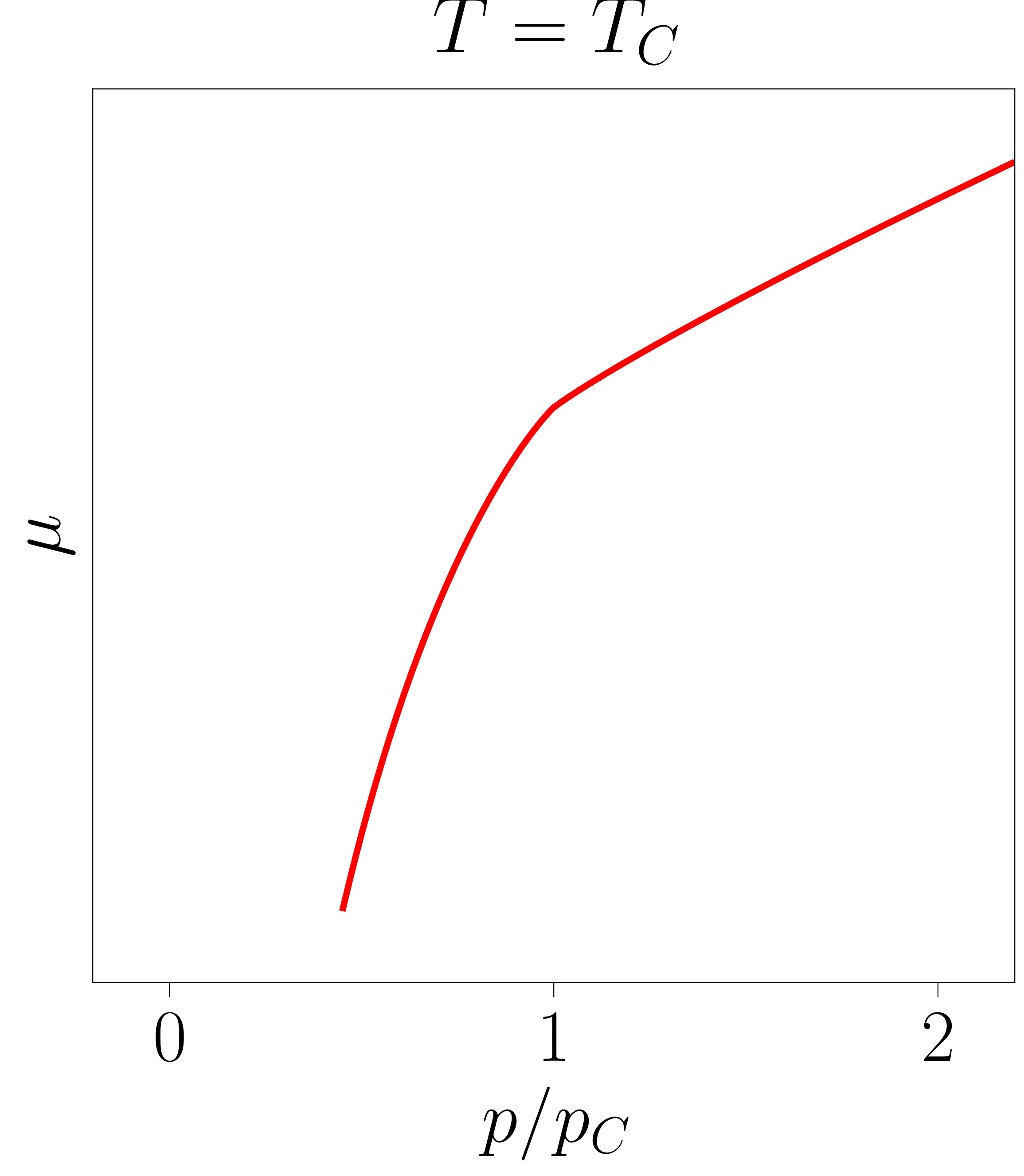
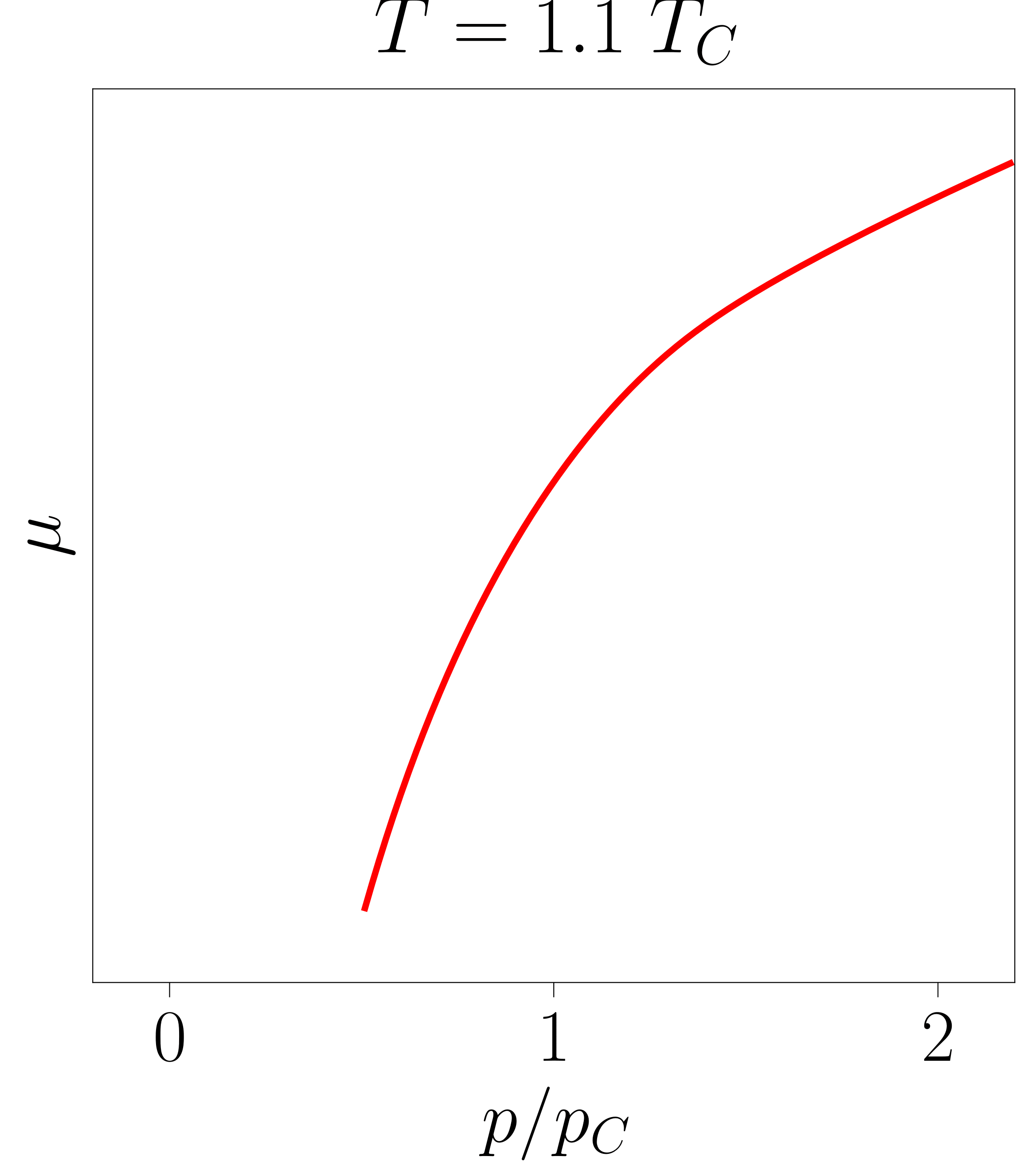
Zenbait tenperaturatan kokatutako sistementzat integral horren balioa kalkulatuz gero (117-000 programan lantzen den moduan), honelako \(\mu\)-ren adierazpenak lortzen dira:

irudia: Tenperatura ezberdinetarako lortutako potentzial kimikoak. Irudiak 117-000 programarekin sortu dira.

Hiru adar bereiz daitezke 4. irudiko lehenengo grafikan: irudiko lehenengo grafikan: lehena, puntu baxuenetik hasita kurbadura negatiboarekin igotzen dena, gas egoerari dagokion potentzial kimikoa da. Bigarrena presio handietan bakarrik topa daitekeen kurba da, hau ere kurbadura negatiboduna eta likido egoeraren potentzial kimikoa adierazten duena.

Bi kurba horiek eskuragarri dauden presioetan kontuan izan behar da sistema beti bi kurbetatik \(\mu\) txikiena duenean egongo dela, aurreko atalean azaldu denez. Ondorioz, \(p\) txikietan sistema gas egoeran egongo da. Bi kurbak elkartzen diren puntuan bien potentzial kimikoak berdinak direnez, sistemak lehen ordenako fase-trantsizioa jasango du. Hortik aurrera sistema likido egoeran egongo da, horri dagokiona izango baita balio baxueneko potentzial kimikoak dituen kurba.

Bi adar horien artekoari dagokionez, azpimarragarria da bere kurbadurak besteek azaltzen dutenaren aurkako zeinua duela. Aurreko atalean aipatutako egonkortasun-baldintzei erreparatuz (ikus \ref{fas-1}. adierazpenak), argi gelditzen da gune horretan sistema ez dela egonkorra eta, ondorioz, sistemak ez duela inoiz hirugarren adar hori jarraituko. Ohartu, 4. irudian potentzial kimikoa aldagai intentsibo baten menpe adierazten dela eta, beraz, sistema egonkorra izan dadin bere bigarren deribatua negatiboa izan behar dela.

Beste bi grafiketan ageri denez, \(T \geq T_C\) kasuetan ez da hirugarren adar hori azaltzen. Ondorioz, sistema egonkorra da eremu guztian eta lehen ordenako fase-trantsizioak jasan beharrean, bigarren ordenakoak jasaten ditu.

Lerro isotermo errealak¶

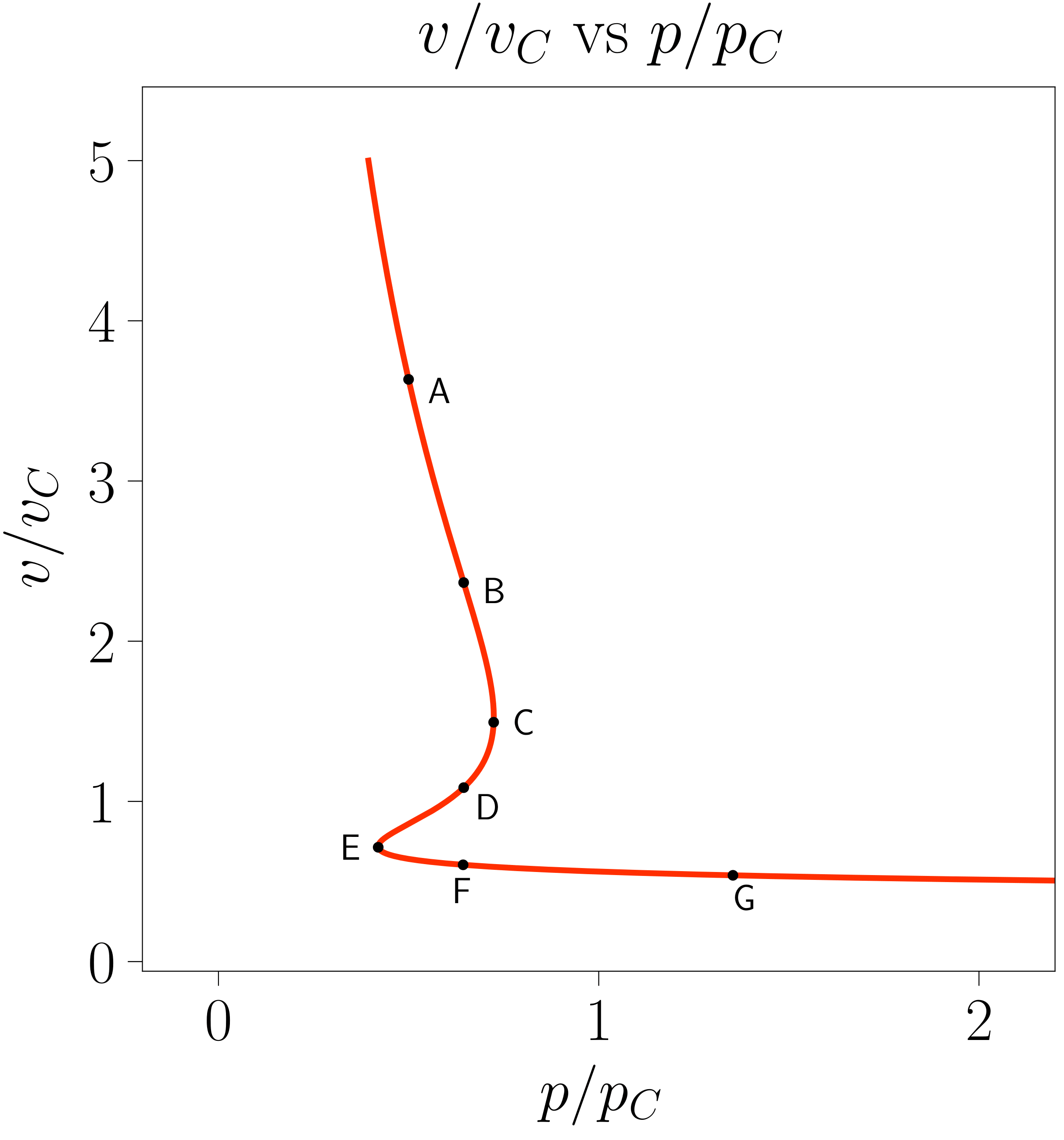
Egonkortasun-baldintzak betetzen diren edozein puntutan topatu daiteke sistema; hau da: posiblea da sistema 5. irudiko C edo E puntuetan topatzea, nahiz eta potentzial kimikoa minimizatzen duten egoerak ez izan. Egoera metaegonkorrak dira horiek: ertan kokatutako sistema batek perturbazio txiki bat jasanez gero, bi fase bereizgarrietan banatuko da.

Sistema C puntuan dagoenean likido gain berotua egoeran dagoela esaten da eta E puntuan aldiz gas azpi hoztua egoeran [3].

Sistema ezin denez egoera ezegonkor batean egon, argi dago ez dela C puntutik E puntura \ref{vdw-7}. irudiko lerro isotermoan zehar joaten eta behin fase-trantsizioa hasita sistema beste lerro isotermo bati jarraitzen diola.

Ideia horretan sakontzeko,117-000 programan \(v = v(p, T)\) grafikako puntuak \(\mu = \mu(p, T)\) grafikako puntuekin zuzenenan erlazionatu daitezke, 7. irudian erakusten denez. Ezkerreko grafikako lerro isotermoan zehar 6. ekuazioko integrala kalkulatuz eskuineko irudiko potentzial kimikoa lor daiteke. Markatutako puntuek esangura berezia dute: lehen azaldutako C eta E puntuez gain, A eta G puntuek sistema fase bakarrean ageri deneko egoerak adierazten dituzte, B eta F puntuek lehen ordenado fase-trantsizioaren muga azaltzen dute eta D puntuak sistema ezegonkorra den egoera adierazten du.

irudia: Potentzial kimikoaren eraikuntza erakusteko sortutako irudiak. Aukeratutako lerro isotermoa \(T = 0.9 \; T_C\) tenperaturari dagokio. Irudiak 117-000 programarekin sortu dira.

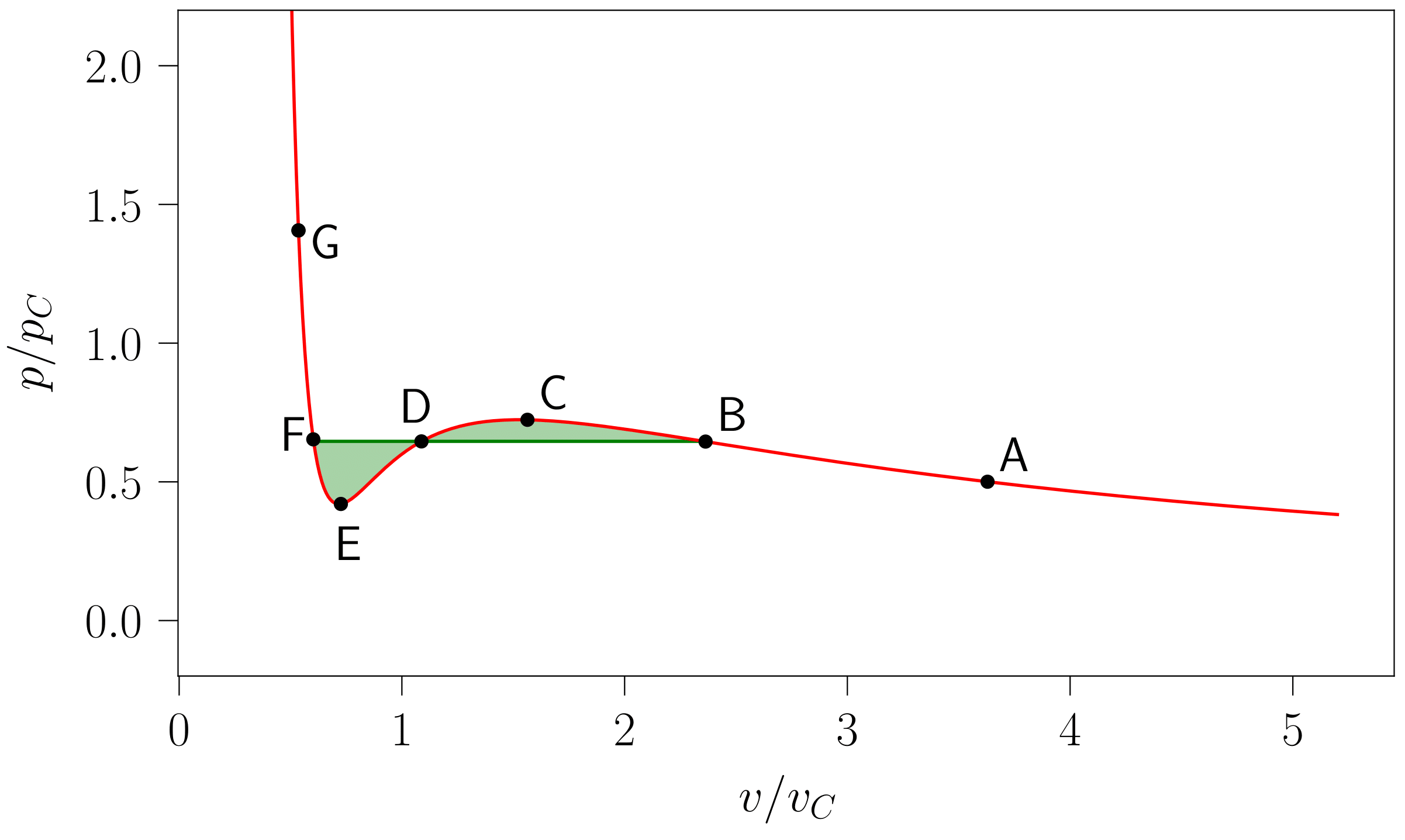
Azaldutako puntu berezi horiek ohiko lerro isotermoaren gainean proiektatu daitezke fase-trantsizioa hasten denean lerro isotermoan gertatzen dena aztertzeko.

irudia: Tenperatura azpikritikodun lerro isotermoa, 5. irudiko grafikak sortzeko erabilitakoa. Koloreztatutako azalerak Maxwell-en eraikuntzari dagokio: sistema tenperatura batean finkatu ostean bi azalera horien balioak berdintzen presioan gertatuko da lehen ordenako fase trantsizioa. Irudia 111-000 programarekin sortu da.

Lehen aipatu denez, bi faseen potentzial kimikoak berdinak direnean gertatuko da lehen ordenako fase-trantsizioa. Ondorioz, B eta F puntuetan \(\mu_1 = \mu_2\) baldintza bete behar da, \(\mu_i\) fase bakoitzari dagokion potentzial kimikoa izanik.

\begin{equation} \mu_1 = \mu_2 \; \rightarrow \; \int_F^B v(p) dp = 0 \end{equation}

Integral hori bi zatitan bana daiteke:

\begin{equation} \int_F^D v(p) dp + \int_D^B v(p) dp = 0 \end{equation}

Hau da, 6. irudian koloreztatutako bi azalerak balioz berdinak izan behar dira. Arau horri Maxwell-en eraikuntza deritzo: sistemaren isoterma erreala trunkatutako isoterma ideala izango da [2].

Sistemaren tenperatura tenperatura kritikoa baino baxuagoa den kasuetan (6. irudikoa, esaterako), sistema G puntutik B puntura van der Waals-ek proposatutako lerro isotermoari jarraituz garatuko da, F-B tartea lerro isobarikoan zehar egingo du eta B puntutik A punturako bidea berriro ere hasierako lerrotik egingo du, trantsizio guztian egonkortasun-baldintza hautsi gabe. Sistema tenperatura kritikoaren gainetik finkatzean, bigarren ordenako fase-trantsizioa van der Waals-en isotermei jarraituz gertatuko da.

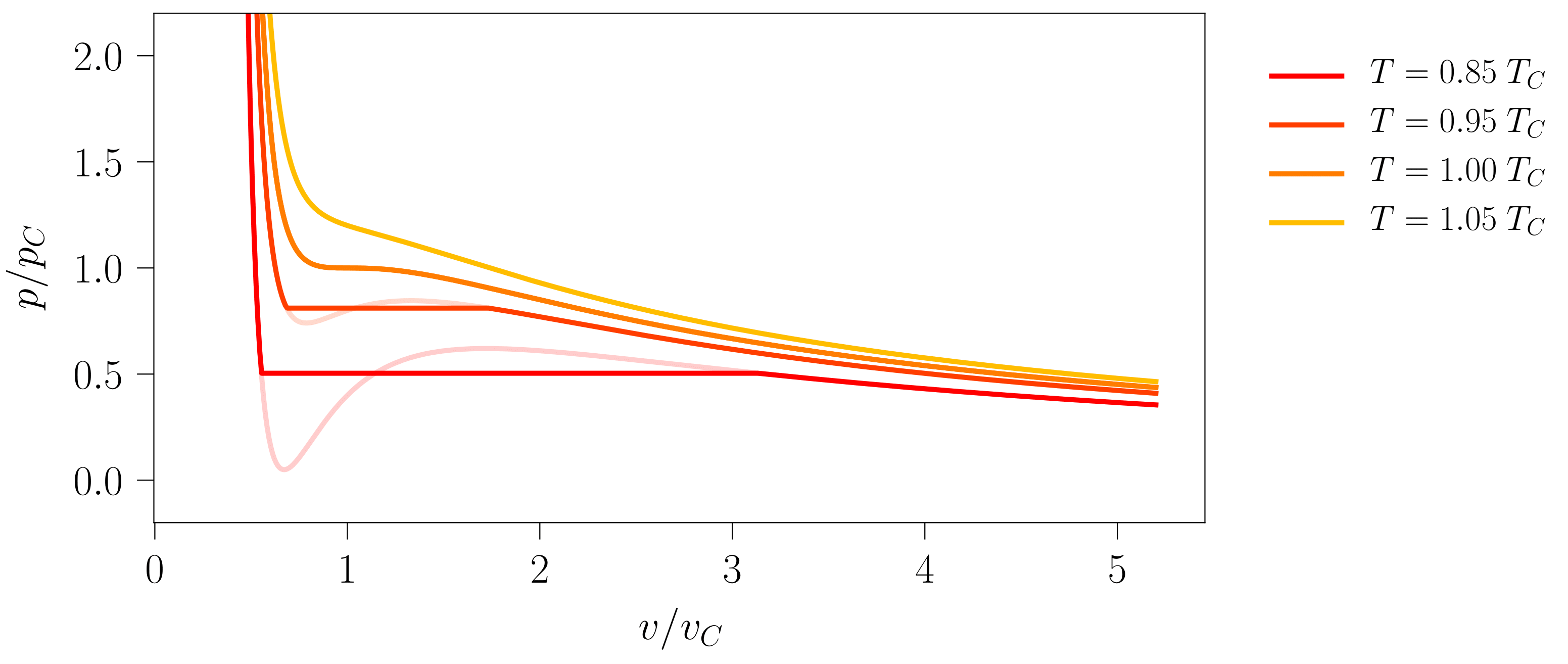
Hori hobeto azaltzeko, 111-000 programaren bidez 7. irudia sortu da. Bertan, zenbait tenperatura ezberdinetan kokatutako sistemek errealitatean izango luketen garapena azaltzen da, Maxwell-en eraikuntzaren bidez kalkulatutakoa. Gainera, \(T < T_C\) kasuetan van der Waals-en lerro isotermo idealak ere adierazten dira, opakutasun txikiagoko lerroen bitartez.

irudia: Zenbait tenperaturatan kokatutako sistema hidrostatiko baten lerro isotermo errealak. Koloreztatutako azalerak Maxwell-en eraikuntzari dagokio: sistema tenperatura batean finkatu ostean bi azalera horien balioak berdintzen presioan gertatuko da lehen ordenako fase trantsizioa. Irudia 111-000 programarekin sortu da.

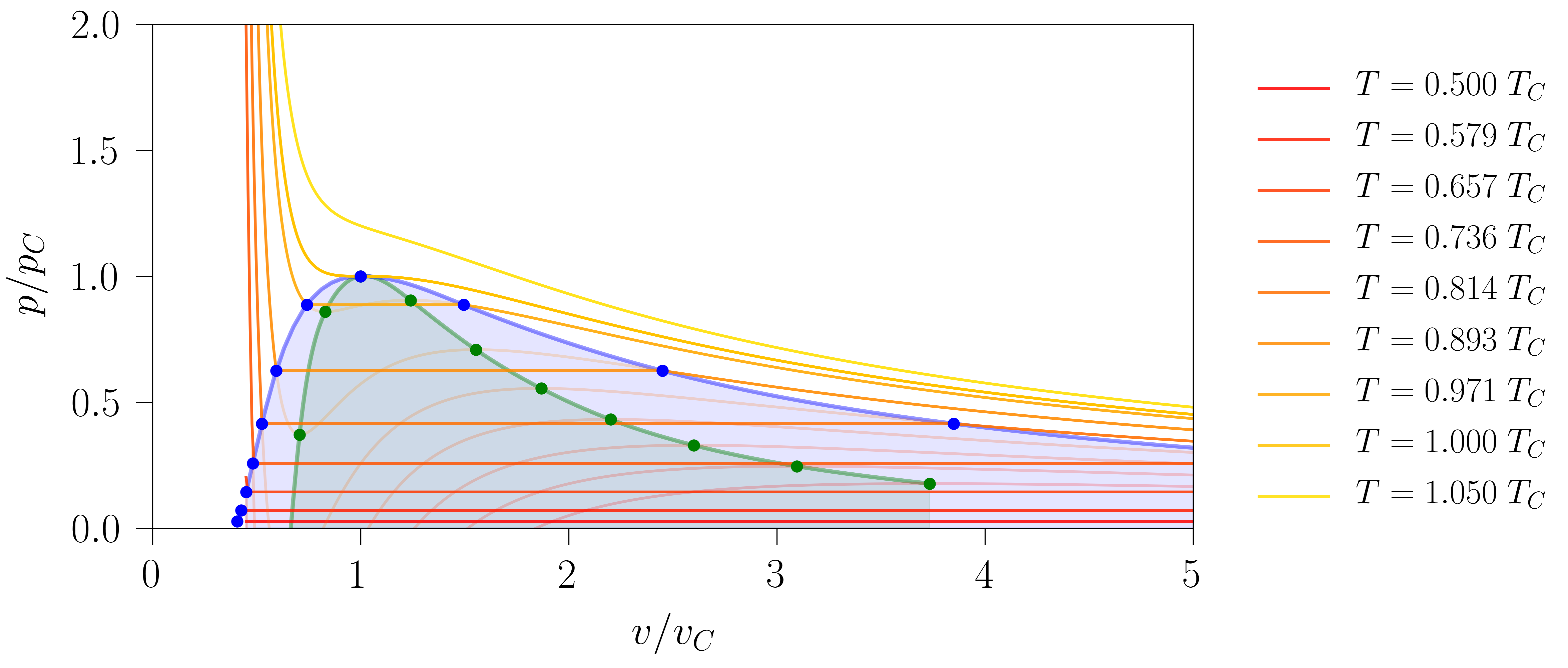
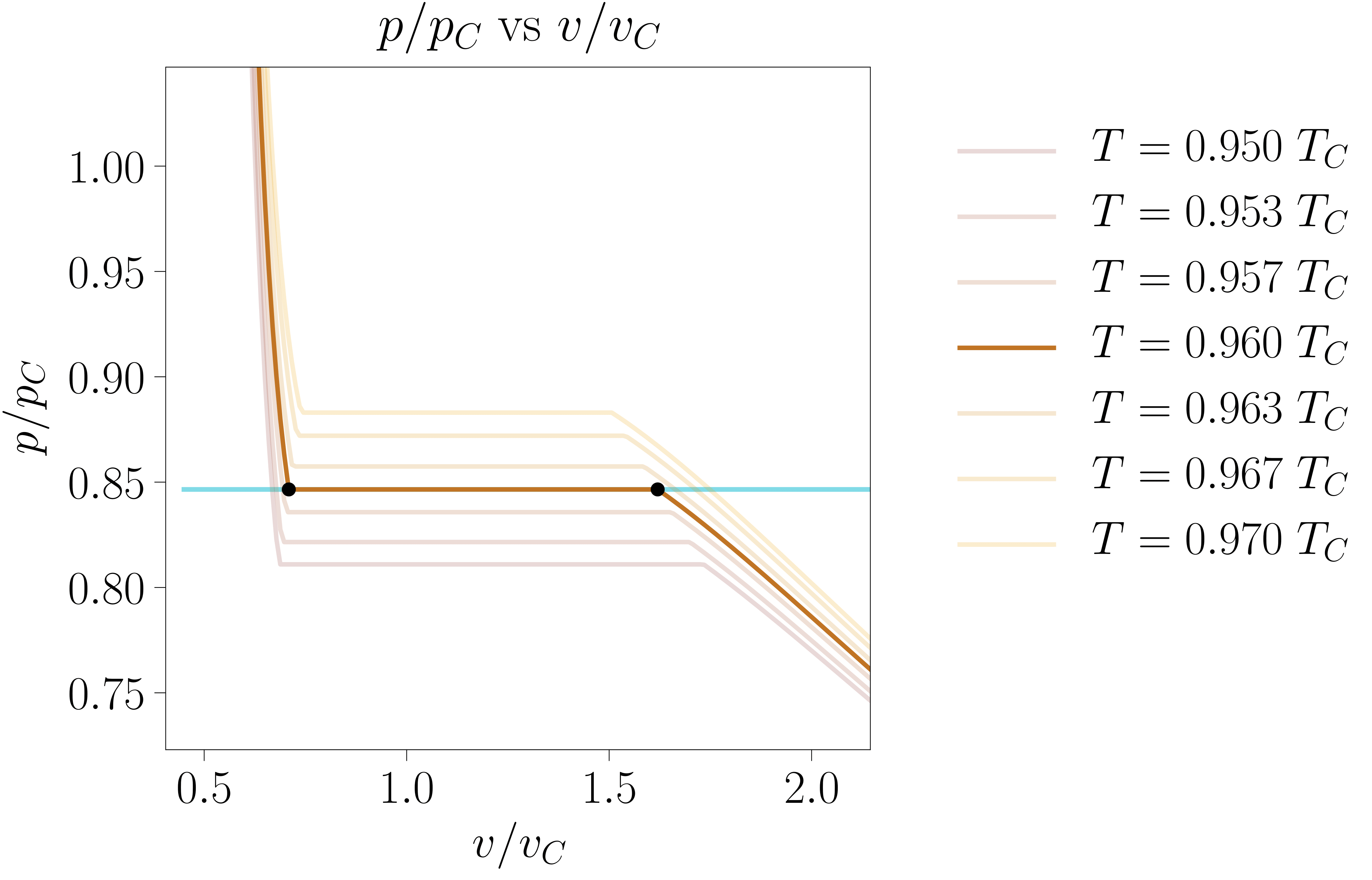
Azterketa hori sakontzeko, tenperatura gehiagotan ipin daiteke sistema, 8. irudian azaltzen den grafika lortuz. Lerro urdinak mugatutako guneari koexistentzia-gunea deritzo: bi fasetan banatuta agertu ohi da bertan kokatutako sistema [2]. Lerro berdeak, aldiz, egonkortasun-baldintzak betetzen ez diren gunea inguratzen du: ezinezkoa da, beraz, berdez koloreztatutako gunean sistema fase bakarrean topatzea. Zonalde urdinean egonkortasun-baldintzak betetzen direnez, baldintza egokiak betez gero, sistema osoa egoera metaegonkor batean ager daiteke [5]. Bi muga horien eta irudikatutako lerro isotermoen arteko ebakidurak puntuek adierazten dituzte.

irudia: Zenbait tenperaturatan kokatutako sistema hidrostatiko baten lerro isotermo errealak. Koexistentzia-gunea urdinez koloreztatu da eta existentziarik gabeko gunea berdez. Koloretako puntuek bi muga horien eta lerro isotermoen arteko ebakidurak adierazten dituzte. Irudia 111-000 programarekin sortu da.

Bolumen molarraren aldaketa¶

Aurreko atalean azaldutako koexistentzia-gunearen mugak sistemaren fase bakoitzeko bolumen molarrak jakiteko erabil daitezke. Lehen aipatu denez, sistema lerro isotermoko eremu isobarikoan zehar garatuko da lehen ordenako fase-trantsizioa jasatean. Trantsizio hori gertatzen den bitartean, fase banatan agertzen den bolumenaren proportzioa palankaren erregela-ren bitartez kalkula daiteke (ikus \ref{palanka}. adierazpena) [2]. Sistemaren bolumen molar osoa \(v\) izanik eta \(v_g\) eta \(v_l\), hurrenez hurren, gas eta likido faseen bolumen molarrak badira, honakoa ondorizta daiteke:

\begin{equation} v = \frac{V}{N} \quad \rightarrow \quad V = v N = N(x_lv_l + x_gv_g) \end{equation}

\begin{equation}\label{palanka} x_l = \frac{v_g - v}{v_g - v_l} \qquad x_g = \frac{v - v_l}{v_g - v_l} \end{equation}

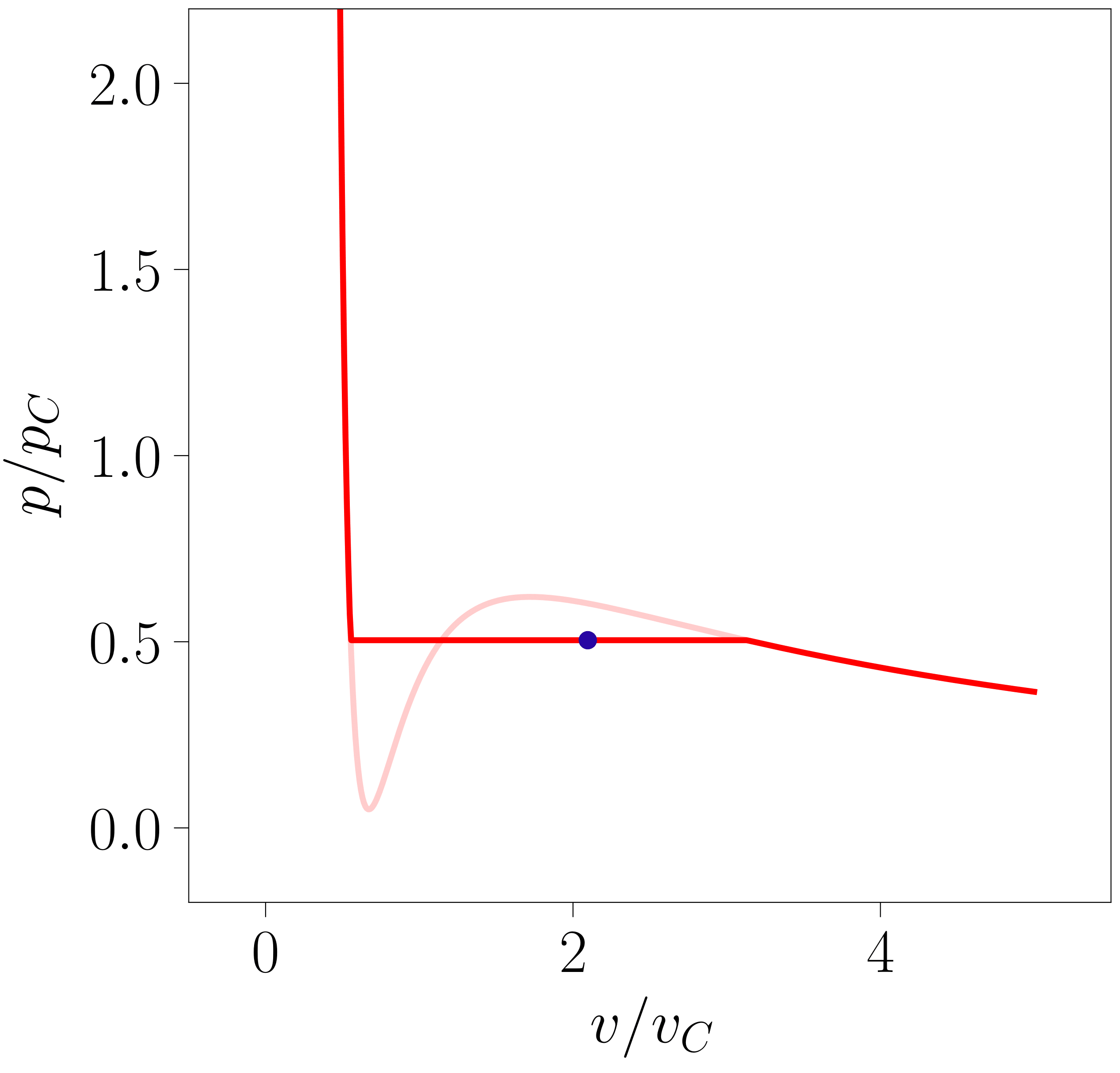
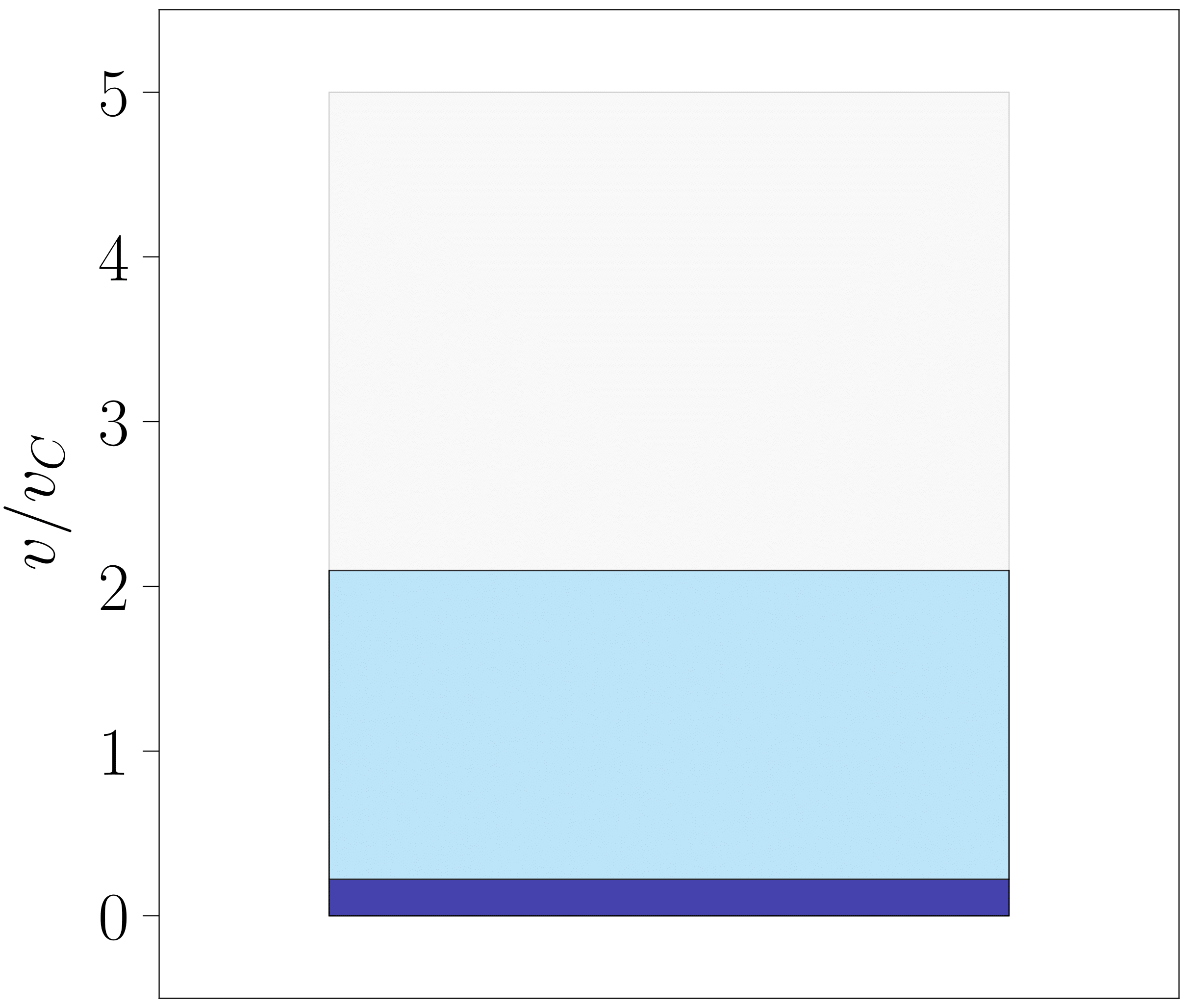
Bi adierazpen horiek oso erabilgarriak izan daitezke likido/gas fase-trantsizioa irudikatzeko, 112-000 programan egin den moduan. Aipaturiko programaz baliatuz 9. irudiko bi diagramak sortu dira. Ezkerrekoan \(T = 0.85 \; T_C\) tenperaturari dagokion sistemaren lerro isotermo esperimental eta teorikoa azaltzen dira (azken hau opakutasun gutxiagorekin). Bertako puntu urdinak sistemaren egoera adierazten du, jatorrizko programan lerro isotermo guztian zehar mugi daitekeena. Eskuinean, aldiz, laborategian behatuko litzatekeenaren diagrama sinplifikatu bat ageri da, puntu urdinak finkatutako egoerari dagokiona hain zuzen ere. Diagramako blokeen koloreak faseen bolumen molarrarekin erlazionatuta daude: urdin argiak gas-faseak betetzen duen bolumen molarra adierazten duen bitartean, ilunak likido-fasearena adierazten du.

irudia: Laborategian sistema hidrostatiko baten fase-trantsizioa lantzean behatuko litzatekeena azaltzeko sortutako irudiak. Kasu honetan \(T = 0.85 \; T_C\) tenperaturan kokatu da sistema. Irudiak 112-000 programarekin sortu dira.

Bigarren grafika horrek jariakinaren portaera esperimentala aurreikusteko aukera ematen du. Presio txikietan sistema gas egoera egongo litzateke (urdin argia) eta presioa handitu ahala gasaren bolumen molarra txikituz joango litzateke fase-trantsizioa hasi arte. Une horretan likido tantak agertuko lirateke (urdin iluna) eta fase-trantsizioak iraun bitartean bi egoeren bolumenen arteko proportzioa palankaren erregelak emandakoa izango litzateke. Sistema osoa fasez aldatzean argi gelditzen da likidoaren konprimagarritasun isotermoa askoz txikiagoa dela, presio aldaketa berdinerako bolumenean eragindako aldaketa lehen baino txikiagoa baita.

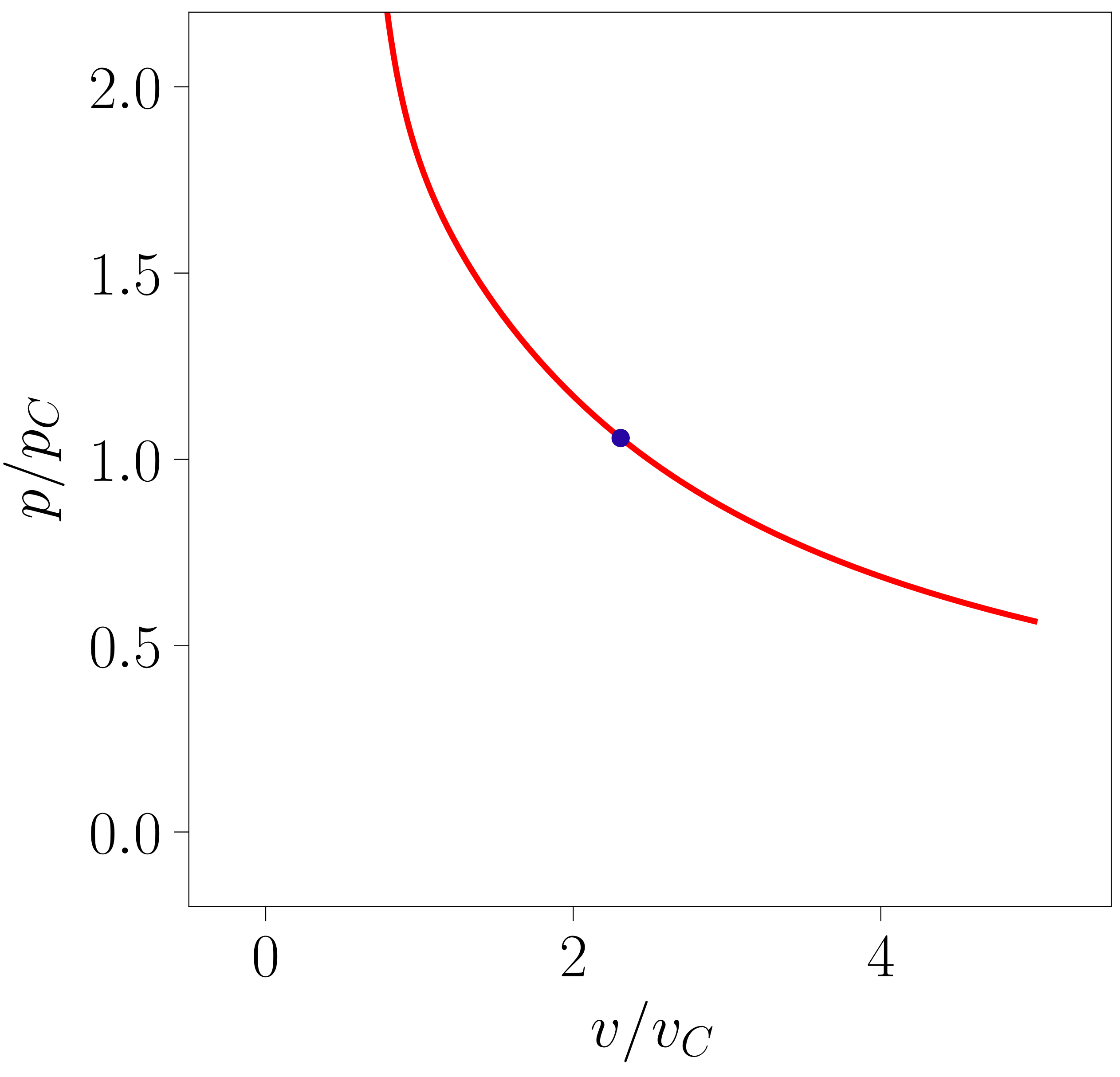
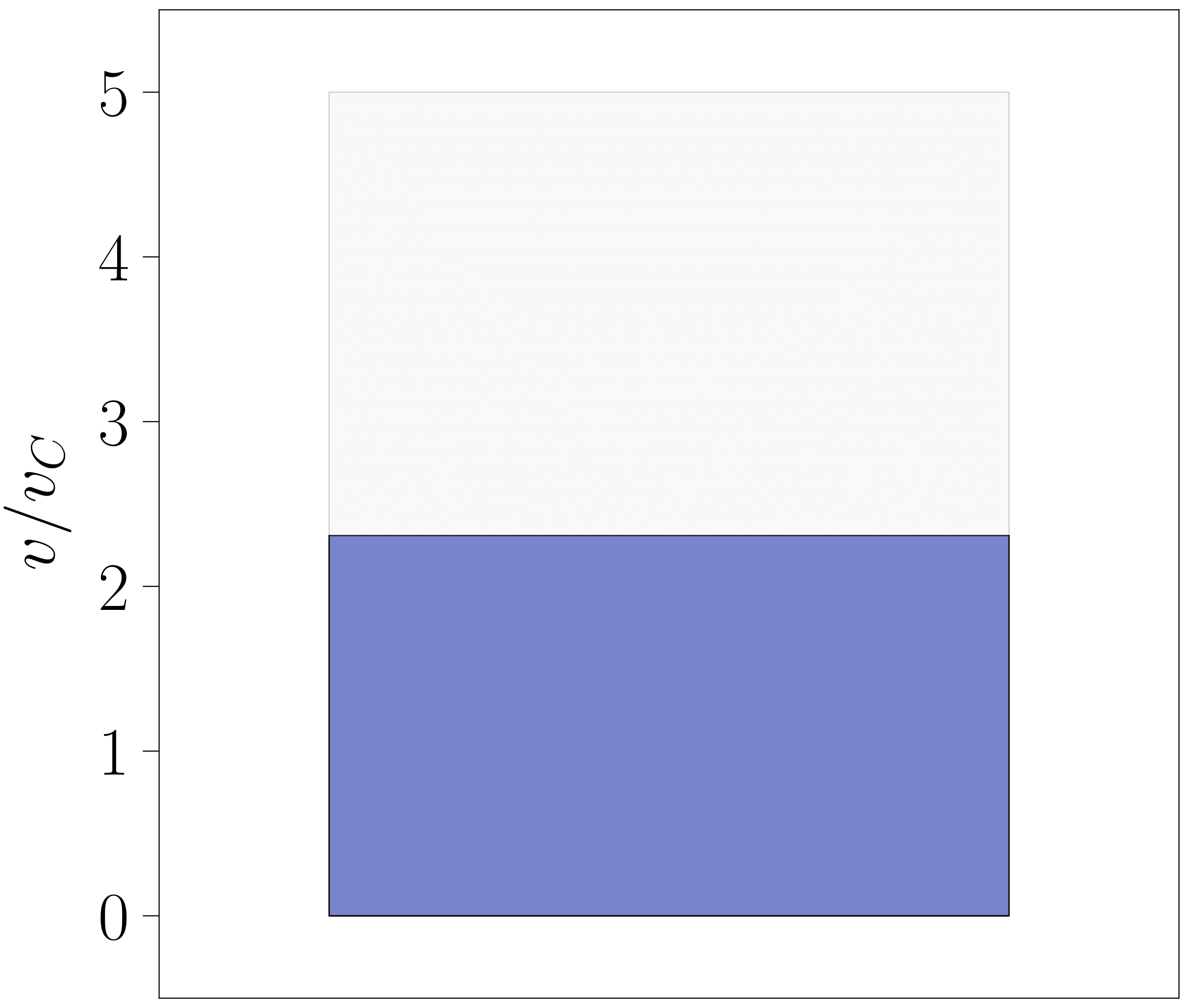
Programa beraz baliatuz, sistema \(T > T_C\) tenperatura batean finkatu eta bigarren ordenako fase-trantsizioen ezaugarriak behatzea ere interesgarria izan daiteke. Kasu horretan, 10. irudian aurkeztutako diagramak lortzeko \(T = 1.2 \; T_C\) tenperaturan finkatu da sistema. Baldintza horren pean sistemak bigarren ordenako fase-trantsizioa jasaten duenez, ez dira aldi berean bi fase bereizi inoiz behatzen: presio baxuko egoera batetik hasi eta presioa pixkanaka handituz, diagramako sistema urdin argiz margotuta egotetik urdin ilunez margotuta egotera pasa da.

Horrek fase-trantsizioen inguruko mezu garrantzitsu bat ematen du, fase-trantsizioen inguruko atalean aipatutakoa: sistema hidrostatikoaren kasuan, lehen ordenako trantsizio batean bolumen molarrak jauzi bat aurkezten du eta bigarren ordenekoetan, aldiz, aipaturiko ezaugarria modu jarraituan garatzen da.

Entropia molarraren aldaketa¶

Bolumen molarraz gain, entropia molarrak ere ez-jarraitasuna azaltzen du lehen ordenako fase-trantsizioetan. Entropiaren adierazpena bere definizioa eta \ref{vdw-8}. ekuazioan aurkeztutako lerro isotermoen adierazpena erabiliz kalkula daiteke.

\begin{equation}\label{vdw-eq-15} ds = \left( \frac{\partial p}{\partial T}\right)_{v} dv \quad \text{eta} \quad p_R \left(v_R, T_R \right) = \frac{8 T_R}{\left(3 v_R - 1 \right)} - \frac{3}{v_R^2} \; \rightarrow \; ds = \frac{8}{3v - 1} \end{equation}

\begin{equation} s = \int \frac{8}{3v - 1} dv = \frac{8}{3} \ln |3v - 1| + \text{kte} \end{equation}

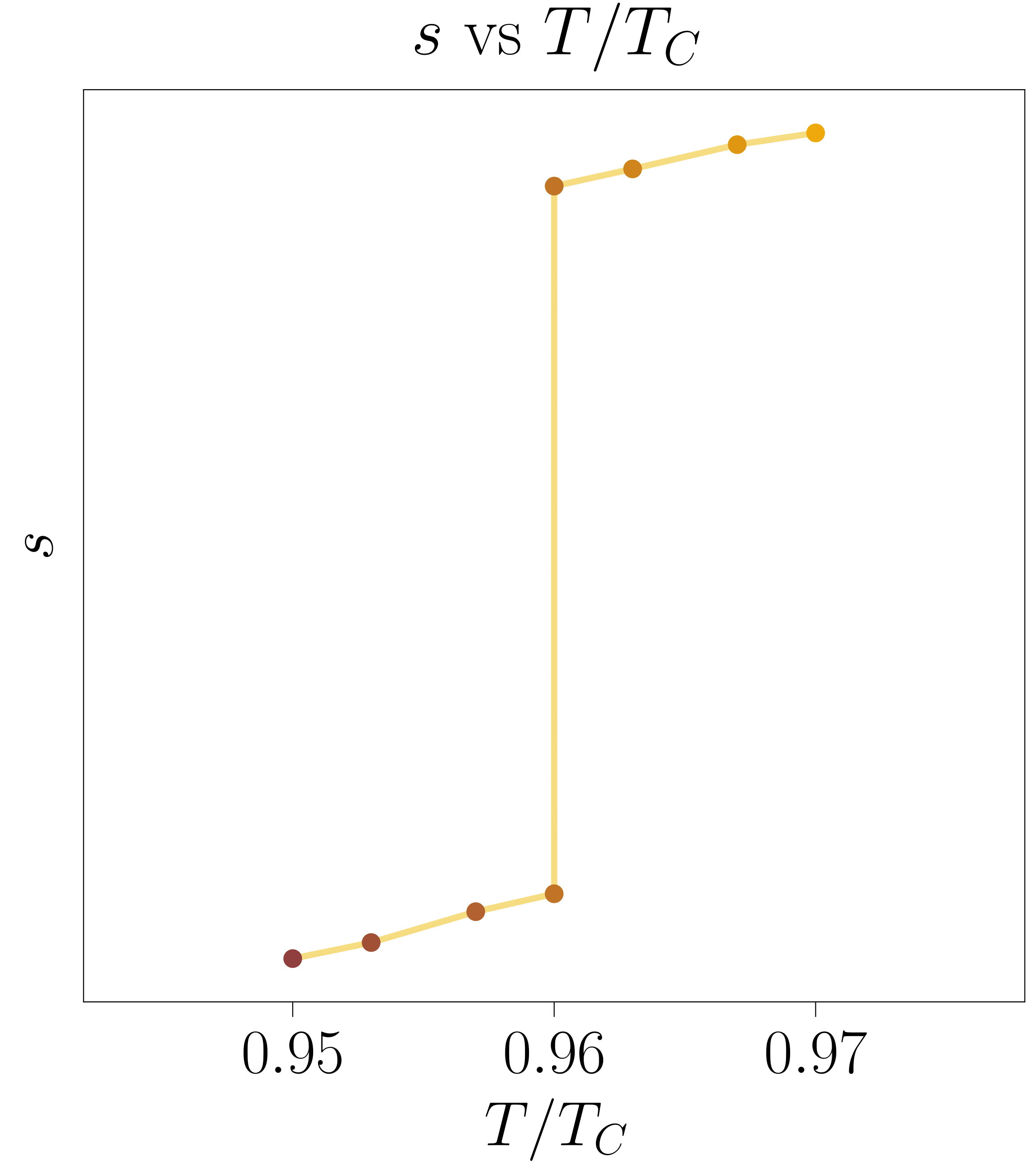
Lortutako adierazpen horrek ez du entropiaren balio absolutua kalkulatzeko balio, baina bere itxura irudikatzeko erabil daiteke (ikus 11. irudia). Oraingoan, sistema tenperatura jakin batean finkatu beharrean presio konstateko baldintzetan mantendu da. Horrela, tenperatura aldatzean, presio eta tenperatura horri dagozkion bolumena hartuko du sistemak. Lehen ordenako fase-trantsizioari dagozkion presio eta tenperaturara iristean, bi bolumen izango ditu eskuragarri, bi faseei dagozkienak, hain zuzen ere. Entropia molarraren bi balio bereizgarri ere izan ahalko ditu, ondorioz. Trantsizioa gertatzen deneko tenperatura gaindituta, sistemak berriro ere entropia bakar bat izango du eskuragarri. Prozesu hau erakusteko 11D-000 programa sortu da, 11. irudiko grafikak egiteko aukera ematen duena.

irudia: Presio konstantean mantendutako sistema baten entropiak tenperaturarekiko duen menpekotasuna azaltzeko sortutako irudiak. Kasu honetan \(T = 1.20 \; T_C\) tenperaturan kokatu da sistema. 11D-000 programarekin sortu dira.

Sistema presio konstantean mantentzen denez, urdinez markatutako lerro isobarikoaren eta bere tenperaturari dagokion lerro isotermoaren arteko ebakiduran egongo da. Ezkerreko grafikan ikusten denez, tenperatura eta presio jakinetan sistemak lehen ordenako fase-trantsizioa jasaten badu, ebakidura horretako puntuen kopurua infinitoa izango da eta sistema ezkerreko grafikan beltzez adierazitako bi egoeren nahasketa bezala agertuko da. Tenperatuta gehiago handituz gero, fase-trantsizioa amaituko da eta sistema osoa fase bakar batean agertuko da (kasu honetan gas egoeran).

Amaitzeko, aipagarria da orain arte azaldutako programa ezberdinak erabiliz fase-trantsizioan gertatutako bero sorra kalkula daitekeela (ikus \ref{vdw-17}. garapena) [2].

\begin{equation}\label{vdw-17} \delta Q = \left(\frac{\partial s}{\partial T}\right) \; \xrightarrow{T = \text{kte}} \; \Delta Q = \frac{1}{T} \; \Delta s = \frac{8}{3T} \ln \left\vert \frac{3v_l - 1}{3v_g - 1} \right\vert \end{equation}

Bibliografia¶

[1] J. D. van der Waals. On the Continuity of the Gaseous and Liquid States. Elsevier Science Publisher B.V., 2004.

[2] Herbert B. Callen. First-order phase transitions in single component systems. In Thermodynamics and an Introduction to Thermostatistics, 215-241 or. Wiley, 2. edizioa, 1985.

[3] Stephen J. Blundell eta Katherine M. Blundell. Real gases. In Concepts in Thermal Physics, 280–288 or. Oxford University Press, 2009.

[4] David R. Lide. Fluid properties. In CRC Handbook of Chemistry and Physics, 43 or. CRC Press, 84. edizioa, 2003.

[5] Pablo G. Debenedetti. Thermodynamics. In Metastable liquids: concepts and principles, Physical chemistry (Princeton, N.J.), 84–88 or. Princeton University Press,1996.